X 3 − x y 2 − 2 x y 2 2 y 3 = x (x 2 − y 2) − 2 y 2 (x − y) after that it's easy to factorize everything Basically the coefficients guide you, you have 3 and 2 and you also have 3 terms you need 4 terms so you can factorize in pairs therefore you must break somehow one of those termsClick here to see ALL problems on Quadratic Equations Question 4623 how do u factor this outhaving trouble x^3 8y^3 Found 2 solutions by longjonsilver, rapaljer Answer by longjonsilver (2297) ( Show Source ) You can put this solution on YOUR website! Which method do you use to factor #3x(x1)4(x1) #?

Factorisation Factorise X Y 3 X Y 3 Factorise X Y 3 X Y 3 Factorisation Class 9 Youtube
(x+y)^3 - (x-y)^3 can be factorised as
(x+y)^3 - (x-y)^3 can be factorised as- How do you factor completely x^3 y^3 z^3 3xyz? 1/y 3 (dy/dx) x1/y 2 = x 3 (1) Put 1/y 2 = z Then2/y 3 (dy/dx) = dz/dx Therefore, Eq (1) becomes 1/2(dz/dx) xz = x 3 ⇒ dz/dx 2xz = 2x 3 It is in the linear form So, the integrating factor e ∫2xdx = ex^2 Multiplying by it, ← Prev Question Next




How To Factorise Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube
Factoring » Tips for entering queries Enter your queries using plain English To avoid ambiguous queries, make sure to use parentheses where necessary Here are some examples illustrating how to ask about factoring factor quadratic x^27x12;Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Get Instant Solutions, 24x7 No Signup required
Factor (xy)^23(yx)^3 Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property Simplify and combine like terms Tap for more steps Simplify each term Tap for more steps Multiply by Factorise (x2y)^3 (2xy)^3 2 See answers tarikh100 tarikh100 Answer 5x)^5 is your answer of your questions above please mark as brainlist and also follow me thank you Answer (x2y)^3(2xy)^3 bas aage nhi aata New questions in MathWhat are the factors of #12x^312x^23x#?
Factorise the following expressions (i) a 2 8 a 1 6 (ii) p 2 − 1 0 p 2 5 (iii) 2 5 m 2 3 0 m 9 (iv) 4 9 y 2 8 4 y z 3 6 z 2 (v) 4 x 2 − 8 x 4 (vi) 1 2 1 b 2 − 8 8 b c 1 6 c 2 (vii) (l m) 2 − 4 l m (viii) a 4 2 a 2 b 2 b 4 Factorise (xy)^3xy 2 See answers report flag outlined bell outlined Log in to add commentAlgebra Factor (xy)^3 (xy)^3 (x y)3 (x − y)3 ( x y) 3 ( x y) 3 Since both terms are perfect cubes, factor using the sum of cubes formula, a3 b3 = (ab)(a2 −abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x y a = x y and b = x− y b = x y




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




X 3 X 2 Factorise Novocom Top
This is the difference of two cubes, ie X^3Y^3 = (XY)(X^2XYY^2) (Learn This) 125x^3−64y^3=(5x)^3(4y)^3 =(5x4y)((5x)^2(5x)(4y)(4y)^2) =(5x4y)(25x^2xy16y^2)Solve for x Use the distributive property to multiply xy by x^ {2}xyy^ {2} and combine like terms Use the distributive property to multiply x y by x 2 − x y y 2 and combine like terms Subtract x^ {3} from both sides Subtract x 3 from both sides Combine x^ {3} and x^ {3} to get 0 Combine x 3 and − x 3 to get 0How do you find the two numbers by using the factoring method, if one number is seven more than




Math 432 Hw 2 5 Solutions Pdf Free Download



How To Factor X Y 3 8 X Y 3 Quora
What are the factors of ( xy)3(x3y3) 2 See answers madhura madhura ⬆️⬆️⬆️Hope This Helps u☺ mahatvisaini007 mahatvisaini007 (x y) (3xy) Hence, one of the factor of given polynomial is 3xy New questions in Math The cost of 4 kg potato, 3kg wheat, and 2 kg rice is rs 60(a) x 2 y 2 2xy (b) x 2 y 2 – xy (c) xy 2 (d) 3xy polynomialsFactorise (X Y)3 8x3 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 5 Question Bank Solutions Concept Notes & Videos 242 Syllabus Advertisement Remove all ads Factorise (X Y)3 8x3 Mathematics




How To Factorise Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Rd Sharma Solutions For Class 8 Chapter 7 Factorization Download Free Pdf
X 3 − 6 y x 8 y 3 1 Find one factor of the form x^ {k}m, where x^ {k} divides the monomial with the highest power x^ {3} and m divides the constant factor 8y^ {3}1 One such factor is x2y1 Factor the polynomial by dividing it by this factor Find one factor of the form x k m, where x k divides the monomial with the highest power x You should be able to identify the curves x 3 y 3 = 91, x y = 1, x y = 7, x y = 13 So because of my relationship to the picture I went to investigating x y = 7 first Just to leave some breadcrumbs about this intuition the black dot is given by ( 91 1 / 3, 91 1 / 3) and this is clearly less than ( 5, 5) so it's not worth1) Factor by grouping x^3 y^3 x^2y xy^2 = (x^3 y^3) (x^2y xy^2) The first is a sum of cubes (x y)(x^2 xy y^2) xy(x y) They both have an x y in common (x y)(x^2 xy y^2) (xy) Now simplify (x y ( x^2 2xy y^2) 2) This is a difference of squares 81x^4




Factor The Gcf 6x 4y 5 15x 3y 2 9x 2y 3




Separating The Varia Bles I 1 Xy 3 Dx 4y Dy Dx 2 Chegg Com
At first glance math(0,1)/math and math(1,0)/math are solutions If it has a nice linear solution, fitting this then that would be mathy= x1/math, lets Which of the following is a factor of (x y) 3 – (x 3 y 3 )? How do you factor #x^3 y^3#?



Cbse 8 Math Ncert Solutions




Factorize 8 X Y 3 27 X Y 3
Do the grouping x 2 y − x 3 − 9 y 9 x = ( x 2 y − x 3) ( − 9 y 9 x), and factor out x 2 in the first and − 9 in the second group Factor out common term xy by using distributive property Factor out common term − x y by using distributive property Consider x^ {2}9 Rewrite x^ {2}9 as x^ {2}3^ {2}11 Factoring x 3 y 3 Theory A difference of two perfect cubes, a 3 b 3 can be factored into (ab) • (a 2 ab b 2) Proof (ab)•(a 2 abb 2) = a 3 a 2 b ab 2ba 2b 2 ab 3 = a 3 (a 2 bba 2)(ab 2b 2 a)b 3 = a 3 0 0b 3 = a 3b 3 Check x 3 is the cubeI'm trying to factorise $$ x^3z x^3y y^3z yz^3 xy^3 xz^3 $$ into four linear factors By plugging it into WolframAlpha I've learned that it's $$(xy)(xz)(yz)(xyz)$$ My question is




Factorisation Factorise X Y 3 X Y 3 Factorise X Y 3 X Y 3 Factorisation Class 9 Youtube



Factorize X X 3 Y 3 3xy X Y Sarthaks Econnect Largest Online Education Community
Expand polynomial (x3)(x^35x2) GCD of x^42x^39x^246x16 with x^48x^325x^246x16Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) ( x y) ( x 2 x y y 2)Step 3 Equation at the end of step 3 (((x 3) ((2•3x 2) • y)) (2 2 •3xy 2)) 2 3 y 3 Step 4 Checking for a perfect cube 41 Factoring x 3 6x 2 y12xy 2 8y 3 x 3 6x 2 y12xy 2 8y 3 is a perfect cube which means it is the cube of another polynomial In our case, the cubic root of x 3 6x 2 y12xy 2 8y 3 is x2y




5 5 Factoring The Sum And Difference Of Two Cubes Ppt Download




The Factors Of X 3 X 2y X Y 2 Y 3 Are A X Y X 2 X Y Y 2 B X Y X 2 X Y Y 2 C Youtube
The expression cannot be factored as it is It is unlikely that you would be presented with a polynomial that cannot be factored I assume that you may have miscopied the problem If we can change thr "3" to a "y", then the following polynomial ca View Full Answer Deep Sah, added an answer, on 3/10/15 Deep Sah answered this We know that a^3 b^3 c^3 3abc = (a b c) (a^2 b^2 c^2 ab bc ac) Take, a = xy, b = yz, c = zx we get, (xy)^3 (yz)^3 (zx)^3 3 (xy) (yz) (zx)Join / Login > 9th > Maths > Polynomials Clearly, 3 x y is factor of (x y) 3 − (x 3 y 3) Option D is correct Answer verified by Toppr Upvote (0) Was this answer helpful?




Factorise 7a 3 56b 3 Maths Questions




Factorise X Cube Minus 2 X Square Y 3 X Y Square Minus 6y Cube Brainly In
This is the Solution of Question From RD SHARMA book of CLASS 9 CHAPTER POLYNOMIALS This Question is also available in R S AGGARWAL book of CLASS 9 You can FWell, can be rewritten as , so we have then There is a standard factorisation forQuestion factor x^3y^3 into irreducibles in Q(x,y) and prove that each of the factors is irreducible Answer by richard1234(7193) (Show Source) You can put this solution on YOUR website!




Factoring And The Factor Theorem Hints To Determine Each Type Ppt Download
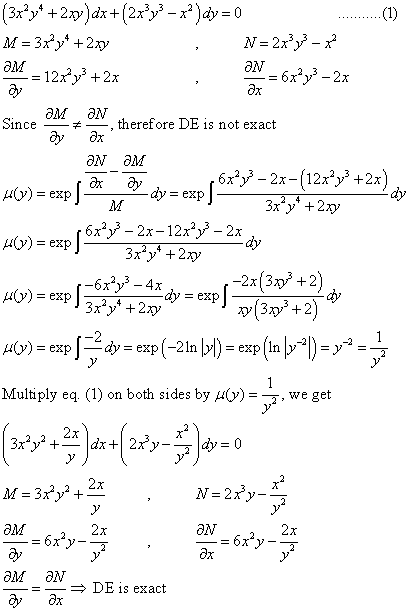



Differential Equations Solved Examples Show That Following Differential Equation Is Not Exact 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Then Find An Integrating Factor To Solve The Differential Equation
(x^3y^3)=(xy)(x^2xyy^2) This is a sum of cubes This is a semiimportant identity to know (x^3y^3)=(xy)(x^2xyy^2) Although it doesn't apply directly to this question, it's also important to know that (x^3y^3)=(xy)(x^2xyy^2) This gives us the rule (x^3y^3)=(xy)(x^2∓xyy^2)Rewrite 6 4 x 3 − y 6 as (4 x) 3 − (y 2) 3 The difference of cubes can be factored using the rule a 3 − b 3 = ( a − b ) ( a 2 a b b 2 ) \left(4xy^{2}\right)\left(16x^{2}4xy^{2}y^{4}\right)Get the answer to this question and access a vast question bank that is tailored for students




Factorise X Y 2x 5 X Y X 3 Maths Factorisation Meritnation Com



Q Tbn And9gcthtcz1praljmvvcvcrjzb8pgvjv5sk9cpymfvv4jfexirrj0rq Usqp Cau
11 Factoring x 3y 3 Theory A difference of two perfect cubes, a 3 b 3 can be factored into a 3b 3 Check x 3 is the cube of x 1 Check y 3 is the cube of y 1 Factorization is (x y) • (x 2 xy y 2) Trying to factor a multi variable polynomial 12 Factoring x 2 xy y 2 Try to factor p ( z) = z 3 − 3 x y ⋅ z x 3 y 3 So we can try our methods to factor a polynomial of degree 3 over an integral domain If it can be factored then there is a factor of degree 1, we call it z − u ( x, y) and u ( x, y) divides the constant term of p ( z) which is x 3 y 3Click here👆to get an answer to your question ️ Which of the following is a factor of (x y)^3 (x^3 y^3) ?




Ex 2 5 9 Verify I X3 Y3 X Y X2 Xy Y2 Ex 2 5




Algebra Ppt Download
Factoring a 3 b 3 An expression of the form a 3 b 3 is called a difference of cubes The factored form of a 3 b 3 is (a b)(a 2 ab b 2) (a b)(a 2 ab b 2) = a 3 a 2 b a 2 b ab 2 ab 2 b 3 = a 3 b 3For example, the factored form of 27x 3 8 (a = 3x, b = 2) is (3x 2)(9x 2 6x 4) Similarly, the factored form of 125x 327y 3 (a = 5x, b = 3y) is (5x 3y)(25x 28x 2 y 3 x 5 = x 2 • (x 3 8y 3) Trying to factor as a Difference of Cubes 32 Factoring x 3 8y 3 Theory A difference of two perfect cubes, a 3 0 0b 3 = a 3b 3 Check 8 is the cube of 2 Check x 3 is the cube of x 1 Check y 3 is the cube of y 1 Factorization is (x 2y) • (x 2 2xy 4y 2) Trying to factor a multiA 3 0 0b 3 = a 3b 3 Check 343 is the cube of 7 Check 27 is the cube of 3 Check x 3 is the cube of x 1 Check y 3 is the cube of y 1 Factorization is (7x 3y) • (49x 2 21xy 9y 2) Trying to factor a multi variable polynomial 32 Factoring 49x 2 21xy 9y 2 Try to factor this multivariable trinomial using trial and error




Solved Factor 2x 14x 12 Completely 2 X 7 X 1 Chegg Com



X Y Z 3 Expansion
This will go according to the formula a^3b^3=(ab)(a^2abb^2) So the solution for the mentioned problem goes like this, the above equation will be converted to the mentioned form a^3b^3 3√3x^3y^3 3=√3*√3=√3^2=3 √3*√3*√3x^3y^3 (√3x) ^3y^3 (√Xy is obviously irreducible For sake of completeness, we show that x^2 xy y^2 is irreducible Suppose that, on the contrary, it is reducibleMove all terms containing X to the left, all other terms to the right Add '3y' to each side of the equation 3X 3y 3y = y 3y Combine like terms 3y 3y = 0 3X 0 = y 3y 3X = y 3y Combine like terms y 3y = 2y 3X = 2y Divide each side by '3' X = y Simplifying X = y




Factorise X 3 Y 3 Novocom Top




Factorize 27 X Y 3 8 X Y 3 Brainly In
Algebra Factor (xy)^3 (xy)^3 (x y)3 − (x − y)3 ( x y) 3 ( x y) 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = xy a = x y and b = x− y b = x y7xy=3 Geometric figure Straight Line Slope = 7 xintercept = 3/7 = yintercept = 3/1 = Rearrange Rearrange the equation by subtracting what isTap for more steps Factor x x out of x 3 x 3 Factor x x out of − 4 x 4 x Factor x x out of x ⋅ x 2 x ⋅ − 4 x ⋅ x 2 x ⋅ 4 Rewrite 4 4 as 22 2 2 Factor




Ex 14 3 2 Iii Divide 8 X 3y 2z 2 X 2y 3z 2 X 2y 2z 3 4x 2




Factorise 8 X Y 3 27 X Y 3 Brainly In
Algebra Polynomials and Factoring Special Products of Polynomials 1 Answer Nghi N #x^3 y^3 = (x y)(x^2 xy y^2)# Answer link Related questions What are the Special Products of Polynomials?




Q 3 Find The Integrating Factor And Solve The Exact Solution Consider The Differential Equation E X Y Cosy Cosx 2e 2x Y Dx Sinx E X Y Siny 3y 2e Y Dy Q 5 Prove Socratic




What Are The Factors Of X Y 3 X 3 Y 3 Maths Polynomials Meritnation Com




Find The Factor Of X Y Cube Minus X Cube Y Cube Brainly In




Find The Special Integrating Factor To Make The Given Chegg Com
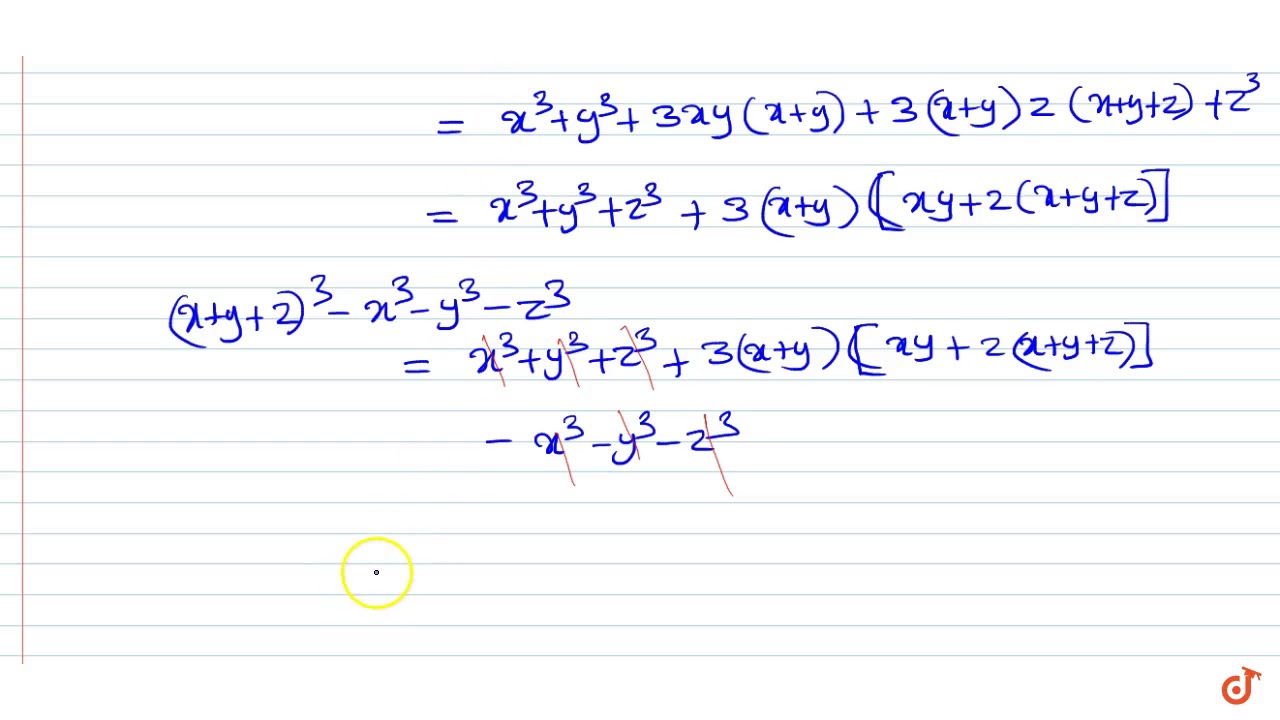



Factorise The Expression X Y Z 3 X 3 Y 3 Z 3 Into Linear Factors Youtube



How To Factorize X Y Y Z Z X Quora



Ml Aggarwal Class 8 Solutions For Icse Maths Chapter 11 Factorisation Check Your Progress




Without Finding The Cubes Factorise X Y 3 Y Z 3 Z X 3 Brainly In




Rd Sharma Solutions For Class 8 Chapter 7 Factorization Download Free Pdf




Simplify X Y X 2 2x 5 2xy X 3 2x 2 3y And Verify Your Result When X Maths Factorisation Meritnation Com




Chapter 6 Review Factor The Expression 1 6x 3 2 X3 4x2 3 4z




8 X Y 3 27 X Y 3 Pleaser Factorise This Maths Polynomials Meritnation Com




Factorise X 5 Y 5
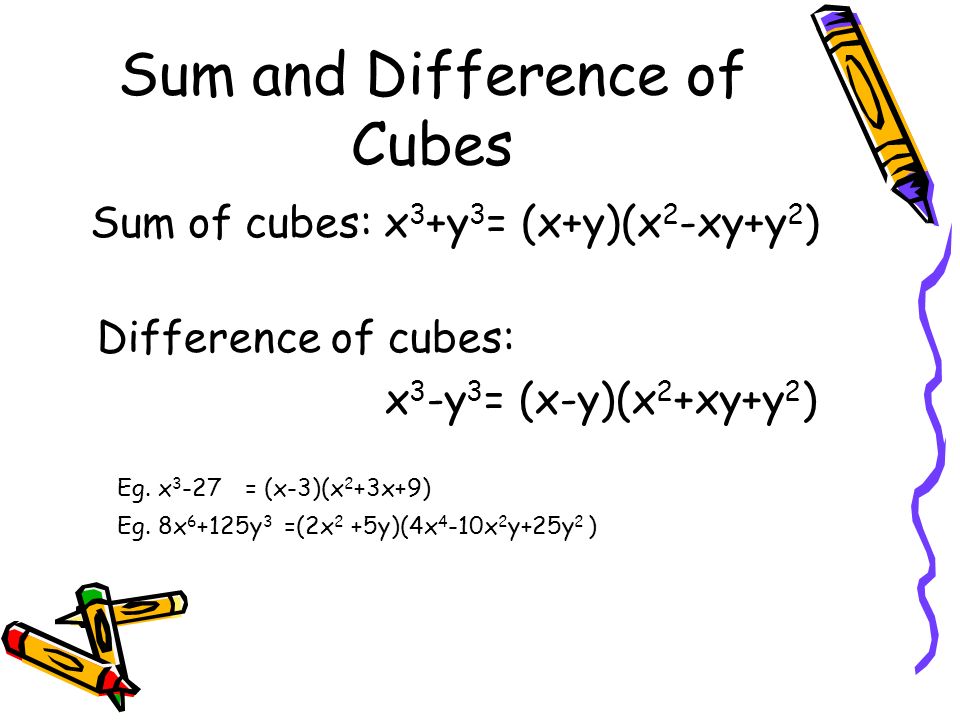



Factoring And The Factor Theorem Hints To Determine Each Type Ppt Download




Factoring And Box Method




Factorise X X 3 3 3x 2y X Y Brainly In




Factorise X Y 3 X Y Brainly In




Factorisation Extra Help And Examples Studocu




Math Problem Factorization X 4y X 2y 3 X 3y 2 Xy 4 Youtube



How To Factor X 3 X 2 Xy X Y 1 Quora



The Differential Equation Math 3dy Dx 3y X 2 X 4 Y 4 Math Is Not Linear What Is The Integrating Factor To Solve This Equation Quora




Factorize X 3y 3 3x Y 3 Brainly In



Factor X 4 X Y 3 X 3 Y 3 Completely Show Your Work Hint First Factor Out A Monomial Brainly Com
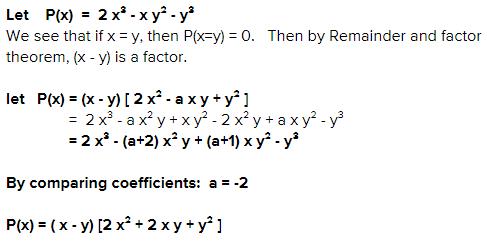



Factorise 2x 3 Xy 2 Y 3 Edurev Class 9 Question




Without Finding The Cubes Factorise X Y 3 Y Z 3 Z X 3 Maths Polynomials Meritnation Com




Which Of The Following Is A Factor Of X Y 3 X 3 Y 3




X 3 3x 2 X 3 Factorise Novocom Top




Factorise X 3 Y 3 Novocom Top



1




Solve For X And Y X Y 3 X 3 Y 2 6 Brainly In




Factorize 27 X Y 3 8 X Y 3 Brainly In




Q27 Q27 X Y 3 X Y 3 Can Be Factorized As Maths Polynomials Meritnation Com




What Are The Factors Of X Y 3 X3 Y3 Brainly In
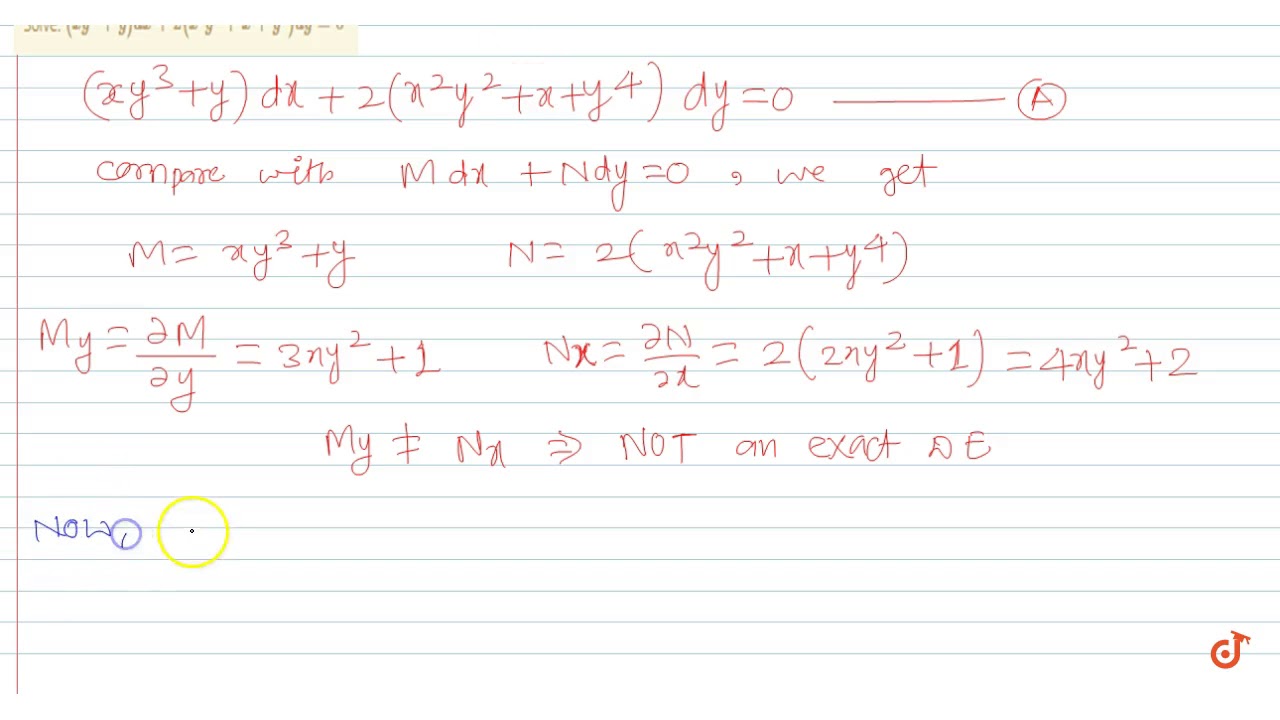



Solve Xy 3 Y Dx 2 X 2y 2 X Y 4 Dy 0 Youtube




How To Factorise Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Ex 14 1 3 I Factorise X 2 X Y 8x 8y Ex 14 1




How To Factor Binomials Factoring Checklist I Binomials




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube




Factorize X X 3 Y 3 3x Y X Y




Copyright C Cengage Learning All Rights Reserved Factoring Polynomials And Solving Equations By Factoring Ppt Download




Factorizing If 2x 1 Is A Factor Of The Expression 6 X2 5x




How To Know At A Glance That Math X 3 3xy 2 2y 3 Math Is Factorable Quora



Cbse 8 Math Ncert Solutions




Which Of The Following Is A Factor Of X Y 3 X 3 Y 3




Ex 14 1 2 Vi Factorise 5 X 2 Y 15 Xy 2 Chapter 14 Class 8



2
.png)



Factorise X3 Y3 Maths Polynomials Meritnation Com



Factorise X X Y 3 3x2y X Mathematics Topperlearning Com




Factorise X Y 3 X 3 Y 3 3xy X Y Brainly In



6 Solve The Following Linear Equations A 2y 1 3 Chegg Com



Ap Calculus Consider Curve Given By Xy 2 X 3 Y 6 Find Dy Dx And Tangent Lines Youtube




Warm Up Exercises Factor Out A Common Binomial Example 1 2x X 4 3 X 4 A 3y 2 Y 2 5 2 Y B Factor 1 From 2 Y Distributive Property Ppt Download




Factorise 27 X 3 Y 3 Z 3 9x Y Z




Math 432 Hw 2 5 Solutions Pdf Free Download




Factor Completely 3y 3 12x 2 Y 7a 3 7 X 3 Chegg Com




Why Is Algebra Fucking Hard Ok Look The Image Below Asks Us To Factor X 2xy Y 9 In The Image Below The Answer Was X Y 3 X Y 3 Unfortunately My Answer




Math 432 Hw 2 5 Solutions




Without Finding The Cubes Factorise X Y Y Z Z X Brainly In




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Factorisation



8p3 Q3 2p 3 Q 3 A3 And We Have A Difference 2p Q 2p 2 2p Q




Factorize 27 X Y 8 2x Y Brainly In




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes



Factorisation De Xy 3 X 2y Y 2 X



Search Q X 5e3 Y 5e3 Formula Tbm Isch
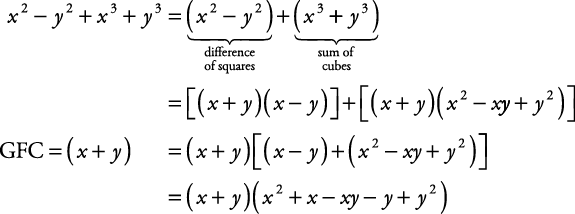



Factoring By Regrouping




Please Quickly Answer Factorise 2x 3 Xy 2 Y 3 Maths Polynomials Meritnation Com




Alevelpure Logarithm Circle



Factorisation Factorise X Y 3 X Y 3 Factorise X Y 3 X Y 3 Factorisation Class 9 Youtube




Factorise X 3 Y 3 Xy X Y



How To Factorise 3 X Y 2 2 X Y Quora




Factorise 8 X Y 3 27 X Y 3 Maths Polynomials Meritnation Com




Simplify 64 X X Y 3 2 Express In Scientific Chegg Com




X 2 Xy 4 Dx 2y 3dy 0 Mathematics Stack Exchange




In Each Of Problems 16 And 18 The Given Copes Is Not Exact But Becomes Exact When Multiplied By The Given Integrating Factor Then Solve The Equation 16 Math 2x 2y 3 X 1 Y 2 Y 0 Math




Factorise 27 X Y 3 8 X Y 3 Maths Polynomials Meritnation Com



0 件のコメント:
コメントを投稿